Inference for two proportions

Warm up

Announcements

Peer review due Sunday at 11:59 pm
If you have not emailed your reviewe yet, do so (and cc me)!

Inference for two proportions

NC poll on equality

A September 16-19, 2023, asked North Carolina voters, among other issues, about issues of equality and women’s progress. Specifically, one of the questions asked:

Which of these two statements come closest to your own views—even if neither is exactly right?

The country has made most of the changes needed to give women equal rights with men.

The country needs to continue to make changes to give women equal rights to men.

STA 101 vs. NC

How do you think the distribution of responses from this class would compare to the NC polling results?

a. Similar distribution of answers between the two polls.

b. Higher percentage of “The country has made most of the changes needed to give women equal rights with men” in STA 101 compared to NC poll.

c. Lower percentage of “The country has made most of the changes needed to give women equal rights with men” in STA 101 compared to NC poll.

Packages

We’ll use the tidyverse and tidymodels packages.

library(tidyverse)
library(tidymodels)

Data

A September 16-19, 2023, asked North Carolina voters, among other issues, about issues of equality and women’s progress. Specifically, one of the questions asked:

Which of these two statements come closest to your own views—even if neither is exactly right?

The country has made most of the changes needed to give women equal rights with men.

The country needs to continue to make changes to give women equal rights to men.

The data from this survey can be found in your data folder: equality.csv.

Hypotheses

Exercise 1

The two populations of interest in this survey are 18-24 year olds and 25+ year olds. State the hypotheses for evaluating whether there is a discernible difference between the proportions of those who think “The country needs to continue to make changes to give women equal rights to men.” (need more changes) in the two age groups.

\(H_0\): There is no difference in how the two groups think about “The country needs to continue to make changes to give women equal rights to men.”

Let \(p\) true population proportion of those who think more changes need to be made.

\(H_0: p_{18-24} = p_{25+}\)

\(H_A: p_{18-24} \neq p_{25+}\)

Sample statistics

Exercise 2

Load the data.

equality <- read_csv("equality.csv")

Exercise 3

Create a 2x2 table of the responses across the two age groups.

equality_table <- equality |>
  count(age, response) |>
  pivot_wider(names_from = "response", values_from = "n")

equality_table

# A tibble: 2 × 3
  age   `Most changes done` `Need more changes`
  <chr>               <int>               <int>
1 18-24                  32                  35
2 25+                   211                 450

Exercise 4

What proportion of 18-24 year olds think “The country needs to continue to make changes to give women equal rights to men”? What proportion of 25+ year olds? Calculate and visualize these proportions.

equality_table |>
  mutate(phat = round(`Need more changes` /(`Most changes done` + `Need more changes`),3))

# A tibble: 2 × 4
  age   `Most changes done` `Need more changes`  phat
  <chr>               <int>               <int> <dbl>
1 18-24                  32                  35 0.522
2 25+                   211                 450 0.681

ggplot(equality, aes(y = age, fill = response)) +
  geom_bar(position = "fill")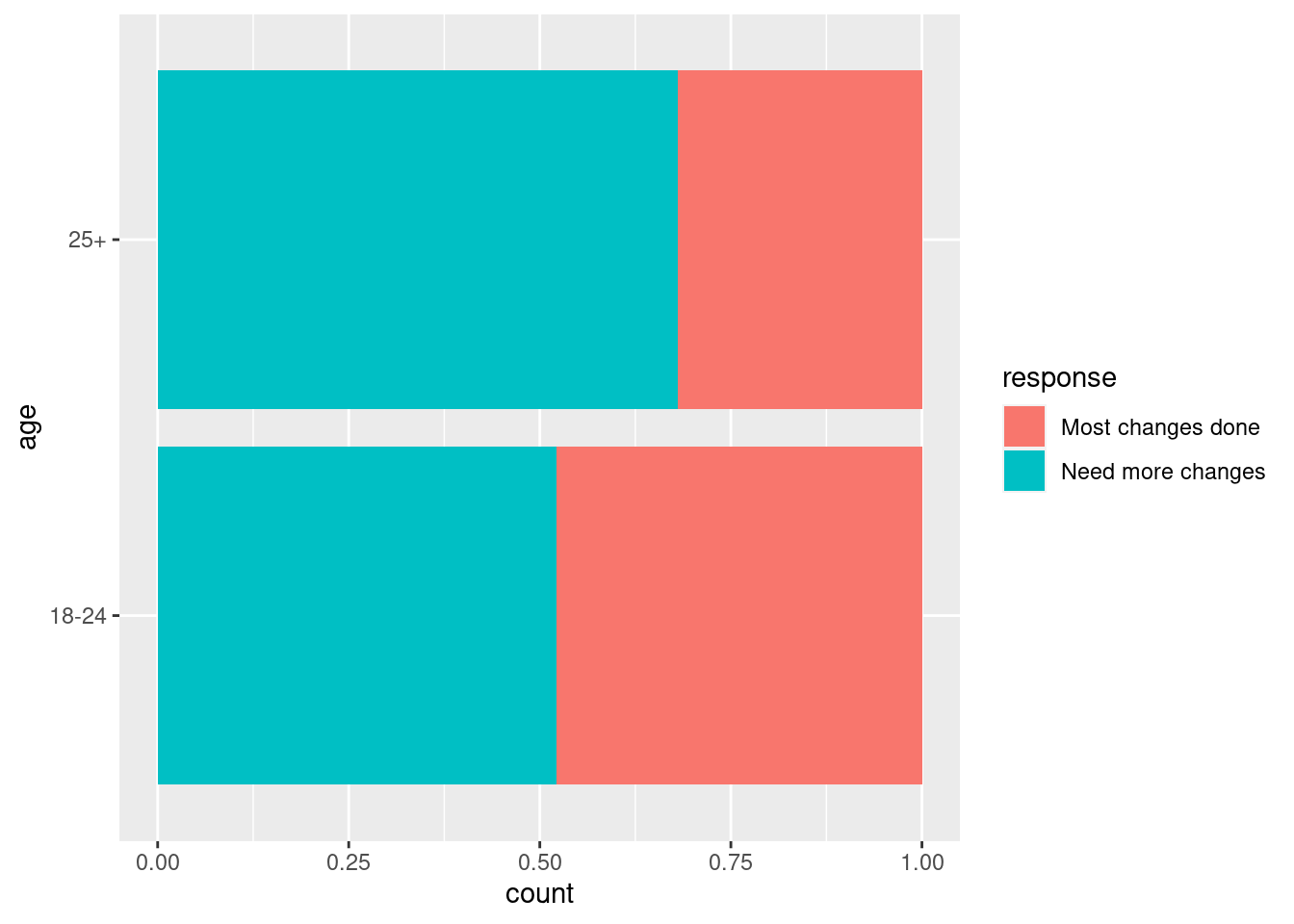

Exercise 5

Calculate the observed sample statistic, i.e., the difference between the proportions of respondents who think “The country needs to continue to make changes to give women equal rights to men” between the two age groups.

obs_stat <- 
  equality |>
  specify(response = response, explanatory = age, success = "Need more changes") |>
  calculate(stat = "diff in props", order = c("18-24", "25+"))

obs_stat

Response: response (factor)
Explanatory: age (factor)
# A tibble: 1 × 1
    stat
   <dbl>
1 -0.158

Testing

Exercise 6

What is the parameter of interest?

Difference between the proportions of those who think “The country needs to continue to make changes to give women equal rights to men” between 18-24 and 25+ year old NC voters.

Exercise 7

Explain how you can set up a simulation for this hypothesis test.

Refer to Chapter 11. Take 485 (35 + 450) white cards and 243 (32 + 211) red cards. Shuffle them. Deal 67 cards into one pile and 661 cards into the second pile. Calculate the proportion of white cards in the first pile minus the proportion of the white cards in the second pile. Repeat many times.

Exercise 8

Conduct the hypothesis test using randomization and visualize and report the p-value.

set.seed(1234)

null_dist <- equality |>
  specify(response = response, explanatory = age, success = "Need more changes") |>
  hypothesise(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  calculate(stat = "diff in props", order = c("18-24", "25+"))

null_dist |>
  get_p_value(obs_stat = obs_stat, direction = "two sided")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.012

null_dist |>
  visualize() +
  shade_p_value(obs_stat = obs_stat, direction = "two sided")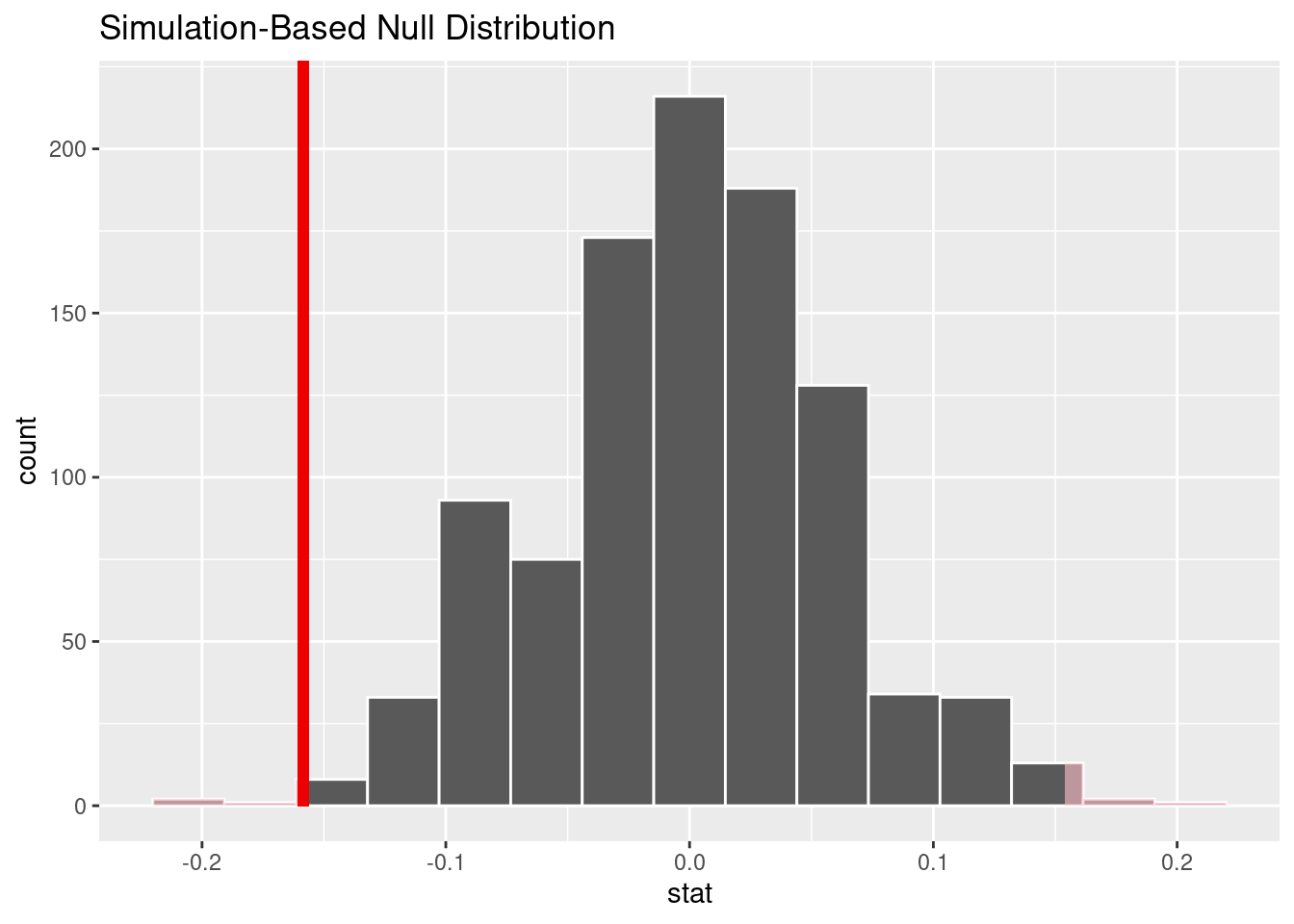

Exercise 9

What is the conclusion of the hypothesis test?

With the p-value of 0.012, which is smaller than 0.05 discernability level, we reject the null hypothesis.

The data provides evidence that there is a difference between the proportion of those who think “The country needs to continue to make changes” in the 18-24 and 25+ groups.

Exercise 10

Interpret the p-value in the context of the data and the hypotheses.

The probability of observing a difference in sample proportions of those who think “The country needs to continue to make changes to give women equal rights to men” between a sample of 67 18-24 year olds and 661 25+ year olds of 0.158 or more (in either direction) is 0.012 if in fact the two population proportions are equal.

Estimation

Exercise 11

Estimate the difference in population proportions of 18-24 year old NC voters and 25+ year old NC voters using a 95% bootstrap interval.

set.seed(1234)

boot_dist <- equality |>
  specify(response = response, explanatory = age, success = "Need more changes") |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "diff in props", order = c("18-24", "25+"))

ci <- boot_dist |>
  get_ci()
ci

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1   -0.288  -0.0279

boot_dist |>
  summarise(quantile(stat, 0.025),
            quantile(stat, 0.975))

# A tibble: 1 × 2
  `quantile(stat, 0.025)` `quantile(stat, 0.975)`
                    <dbl>                   <dbl>
1                  -0.288                 -0.0279

visualise(boot_dist) +
  shade_ci(ci)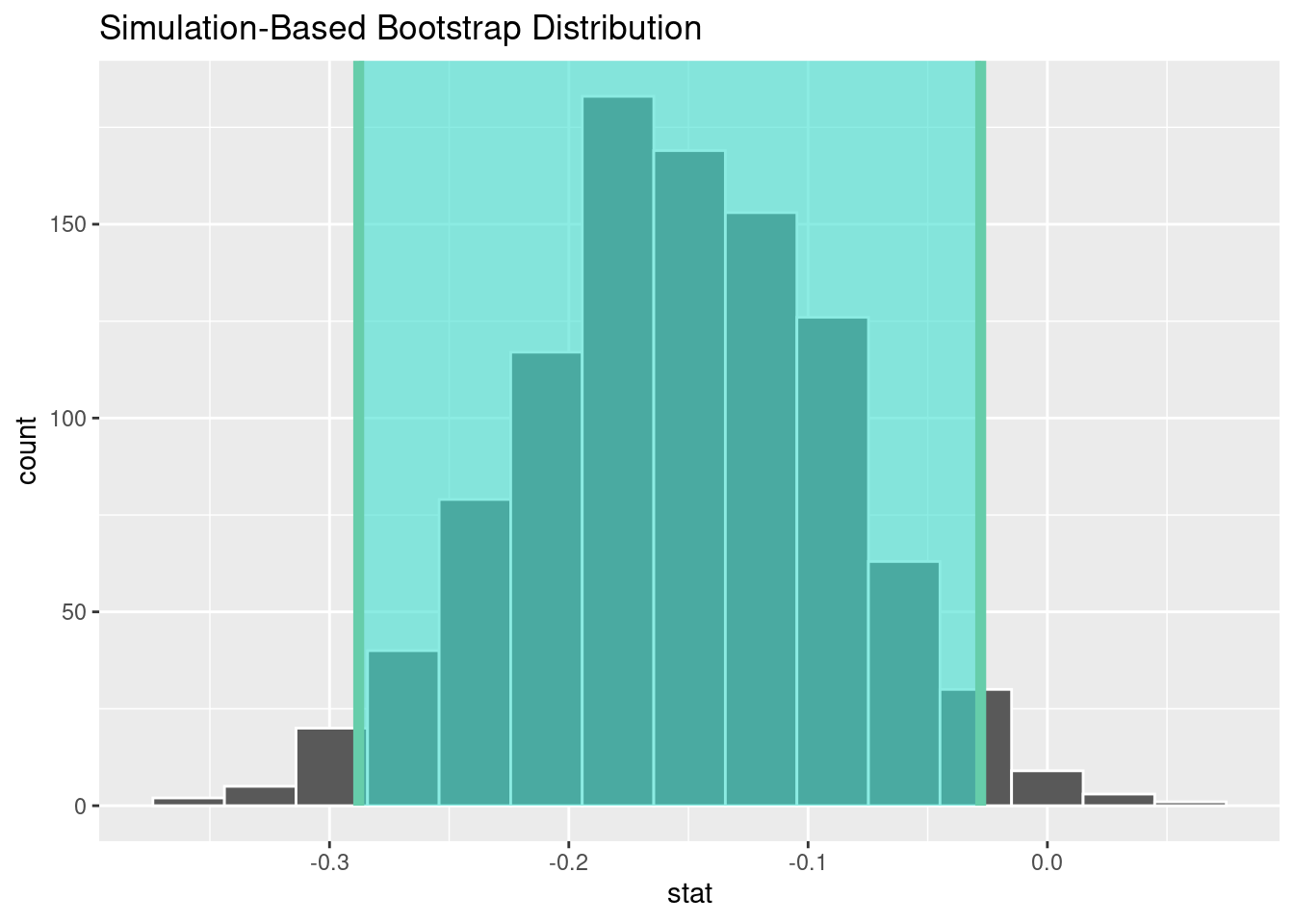

Exercise 12

Interpret the confidence interval in context of the data.

We are 95% confident that the proportion of 18-24 year old NC voters who think “The country needs to continue to make changes to give women equal rights to men” is 28.8% to 2.9% lower than 25+ year old NC voters who share this opinion.

Exercise 13

Describe how the simulation scheme for bootstrapping is different than that for the hypothesis test.

For bootstrap, we sample with replacement from our sample under the assumption that our sample is representative of population.

For hypothesis test, we sample under the assumption that the null is true.

Conceptual

Exercise 14

What is \(p\) vs. \(\hat{p}\) vs. p-value. Explain generically as well as in the context of these data and research question.

\(p\) - population proportion

\(\hat p\) - sample proportion

\(p\)-value - probability of observing our observed sample statistic or something more extreme if null is true.

Exercise 15

What is sampling distribution vs. bootstrap distribution vs. null distribution? Explain generically as well as in the context of these data and research question.

Suppose we have a sample of size \(n\).

Sampling distribution: if we were to collect many samples of size \(n\) from the population and calculate sample statistic for each, how would they be distributed?

Bootstrap distribution: “collect” a sample of size \(n\) by performing sampling with replacement from our sample. Calculate sample statistic on each sample and look at how they are distributed.

Null distribution: assume null is true. Then, we have a “population” to sample from. Generate a sample of size \(n\) under the null assumption and calculate sample statistic for each, how would they be distributed?