Hello data - filled in notes

Announcements

  1. Office hours are updated with minor changes on the course website .
  2. If you haven’t yet done so, please:
    • complete the Getting to know you survey
    • read through the syllabus

Goals

By the end of this class you will

  • meet the computational toolkit for the course
  • practice using glimpse(), names(), nrow(), ncol(), count()
  • define and compute various statistics
  • begin to gain familiarity with making data visualizations with ggplot()

We will do this using water lead content data from Flint, MI. The following paragraph will be useful in evaluating the lead amount values we’ll see in the dataset.

While there is no completely safe amount of lead consumption, the limit allowed by the Lead and Copper Rule (LCR) of 1991 is 15 parts per billion (ppb). If this is exceeded in more than 10% of homes tested (or if the 90th percentile value of the total sample is above 15 ppb), action is required. And to make sure problems are caught, sampling for lead in water is supposed to target the “worst-case” homes – those in areas served by lead pipes.

Meet the toolkit

RStudio

  • Files, plots, viewer, environment, etc. panes

  • Console

  • Editor

R

  • Writing code in the console

  • Basic math with R

    1+2*(3+5)
    [1] 17

  • Creating variables in R, the assignment operator (<-), and the Environment pane

    age <- 27

age + 4
    [1] 31
    age + 9
    [1] 36

  • R functions and packages and the Packages pane

  • Getting help with R and the Help pane

Quarto

  • YAML: Metadata

  • Narrative: Edited with the visual editor (or the source editor)

  • Code: In code chunks

    • Chunk options (following #|)

    • Comments (following #)

    • Code

  • Running individual code chunks vs. rendering a document

Back to analysis

Load packages

We’ll use the tidyverse package for analysis, which offers functionality for data import, wrangling, visualization, and more.

# load a package

library(tidyverse)
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.4.4     ✔ tibble    3.2.1
✔ lubridate 1.9.2     ✔ tidyr     1.3.0
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ purrr::%||%()   masks base::%||%()
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Loading this package prints out a message. What does this message mean? How can we suppress the message from the output?

Load data

The read_csv() function can be used for reading CSV (comma separated values) files. The file we’re reading is called flint with the suffix (.csv) which indicates its file type.

flint <- read_csv("flint.csv")
Rows: 813 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): draw
dbl (4): id, zip, ward, lead

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
view(flint)

One of two things may have happened:

  1. The file was read successfully and you now see a dataset called flint in your Environment pane.
  2. The file was not read successfully and you see an error Error in read_csv("flint.csv") : could not find function "read_csv".

If (1) happened, great!

If (2) happened, let’s troubleshoot first before continuing.

Data dictionary

The following variables are in the flint data frame:

  • id: sample ID number (identifies the home)
  • zip: ZIP code in Flint of the sample’s location
  • ward: ward in Flint of the sample’s location
  • draw: which time point the water was sampled from
  • lead: lead content in parts per billion (ppb)

Populations and samples

We want to learn about the population using a sample.

In the case we want to learn about the lead content in all of Flint, MI homes but only have available water readings from a sample of homes (our data set).

Exercise 1: Look at the data, how many observations are there? How many variables?

nrow(flint)
[1] 813
ncol(flint)
[1] 5

There are 813 observations and 5 variables.

Frequencies

Let’s count() to find the number of different time points water was sampled with the count() function.

  • The first argument is flint: the data frame

  • The second argument is draw: the variable

count(flint, draw)
# A tibble: 3 × 2
  draw       n
  <chr>  <int>
1 first    271
2 second   271
3 third    271

We can achieve the same result with the following “piped” operation as well.

  • The first line is flint: the data frame

  • Then the pipe operator, read as “and then”, which places what comes before it as the first argument of what comes after it

  • The second line is count(draw)

flint |>
  count(draw)
# A tibble: 3 × 2
  draw       n
  <chr>  <int>
1 first    271
2 second   271
3 third    271

We can use a similar approach to fund out how many unique homes are in the data set:

flint |>
  count(id)
# A tibble: 269 × 2
      id     n
   <dbl> <int>
 1     1     3
 2     2     3
 3     4     3
 4     5     3
 5     6     3
 6     7     3
 7     8     3
 8     9     3
 9    12     3
10    13     3
# ℹ 259 more rows

Exercise 2: How many samples were taken from each zip code?

flint |>
  count(zip)
# A tibble: 8 × 2
    zip     n
  <dbl> <int>
1 48502     3
2 48503   207
3 48504   165
4 48505   144
5 48506   132
6 48507   153
7 48529     3
8 48532     6

Exercise 3: Which ZIP code had the most samples drawn? Hint: See the help for count.

flint |>
  count(zip, sort = TRUE)
# A tibble: 8 × 2
    zip     n
  <dbl> <int>
1 48503   207
2 48504   165
3 48507   153
4 48505   144
5 48506   132
6 48532     6
7 48502     3
8 48529     3

Summarization

What is a statistic? It’s any mathematical function of the data. Sometimes, a statistic is referred to as “sample statistic” or “summary statistic”, since you compute it from a sample (the observed data) and not the entire population.

Measures of central tendency

  • mean
  • median
  • mode

Measures of spread

  • variance
  • standard deviation
  • range
  • quartiles
  • inter-quartile range (IQR)

Order statistics

  • quantiles
  • minimum (0 percentile)
  • median (50th percentile)
  • maximum (100 percentile)

… and any other arbitrary function of the data you can come up with!

Exercise 4: Compute each of these statistics for lead ppb.

summary_table <- flint |>
  summarize(mean_lead = mean(lead),
            median_lead = median(lead),
            var_lead = var(lead),
            sd_lead = sd(lead))
summary_table
# A tibble: 1 × 4
  mean_lead median_lead var_lead sd_lead
      <dbl>       <dbl>    <dbl>   <dbl>
1      8.20        1.85    1718.    41.5

Plotting

Histograms

Let’s take a look at the distribution of lead content in homes in Flint, MI.

ggplot(flint, aes(x = lead)) +
  geom_histogram()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.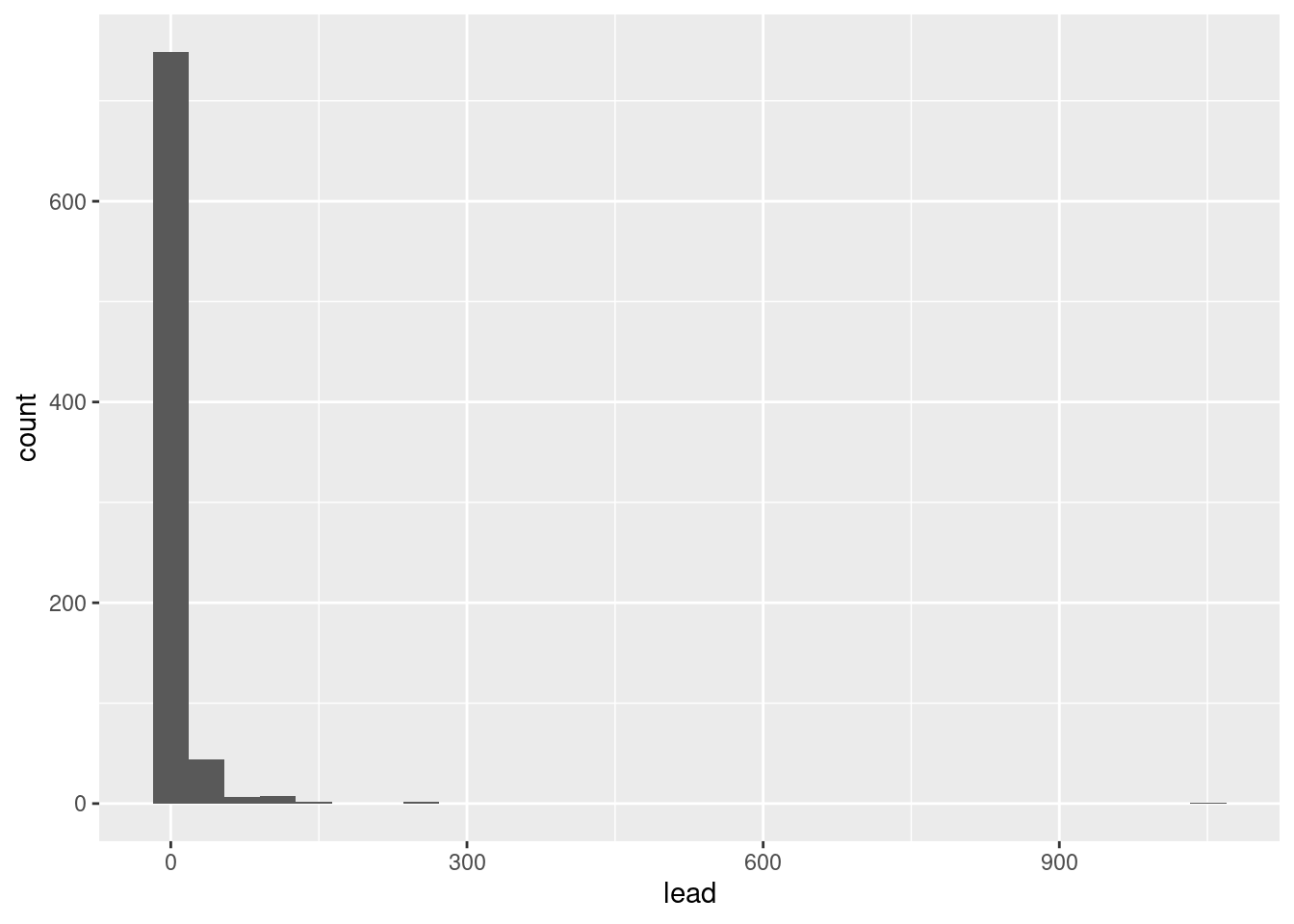

We can make this plot look nicer/more useful by adjusting the number of bins and zooming into the x-axis.

ggplot(flint, aes(x = lead)) +
  geom_histogram(bins = 50) +
  coord_cartesian(xlim = c(0, 100))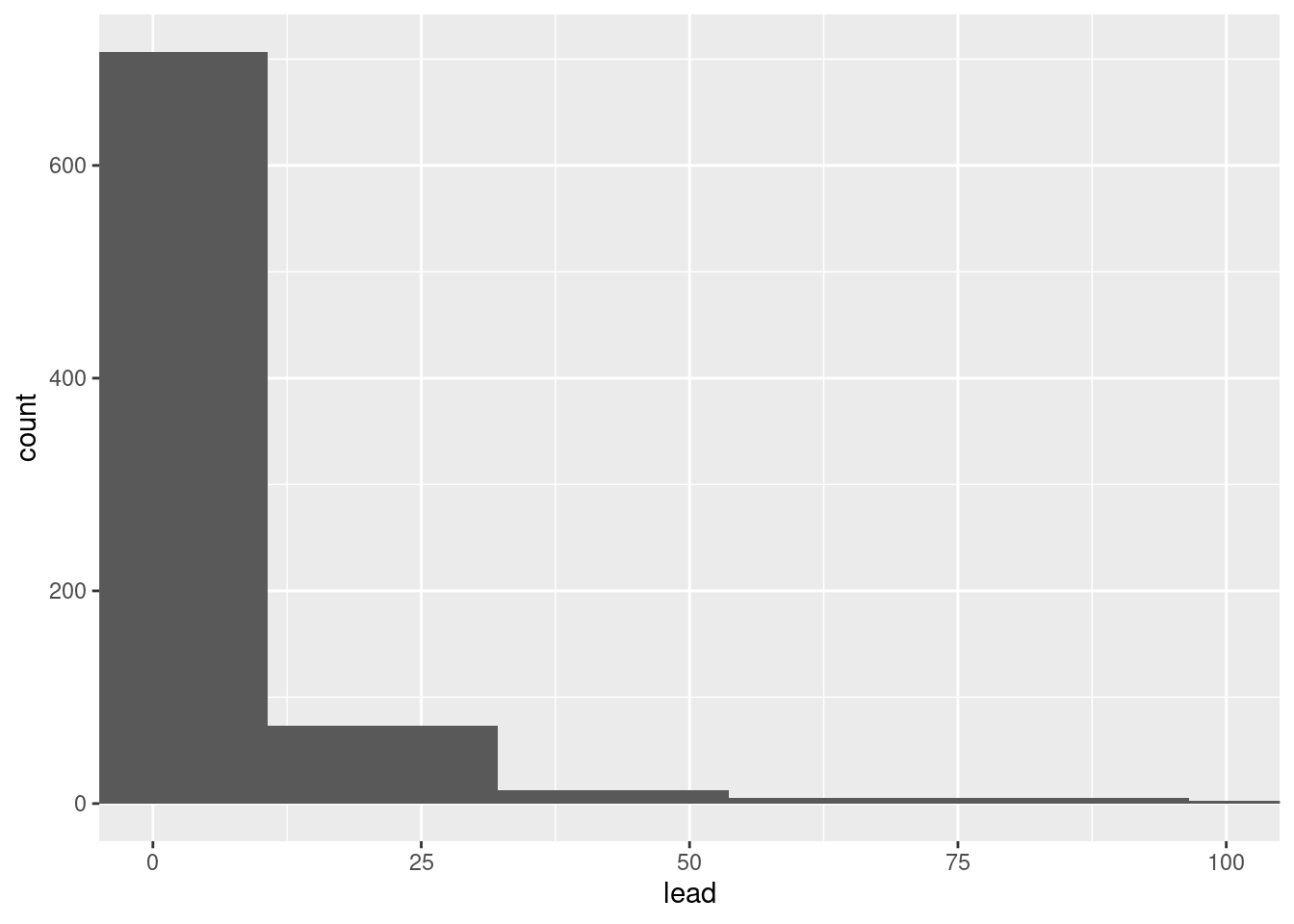

Let’s visualize some of our summary statistics on the plot.

Exercise 5: Add a new layer, geom_vline(xintercept = __, color = "red"), to the histogram below, filling in the blank with the mean.

mean_lead <- mean(flint$lead)


ggplot(flint, aes(x = lead)) + 
  geom_histogram(bins = 50) + 
  coord_cartesian(xlim = c(0, 100)) +
  geom_vline(xintercept = summary_table$mean_lead, color = "red")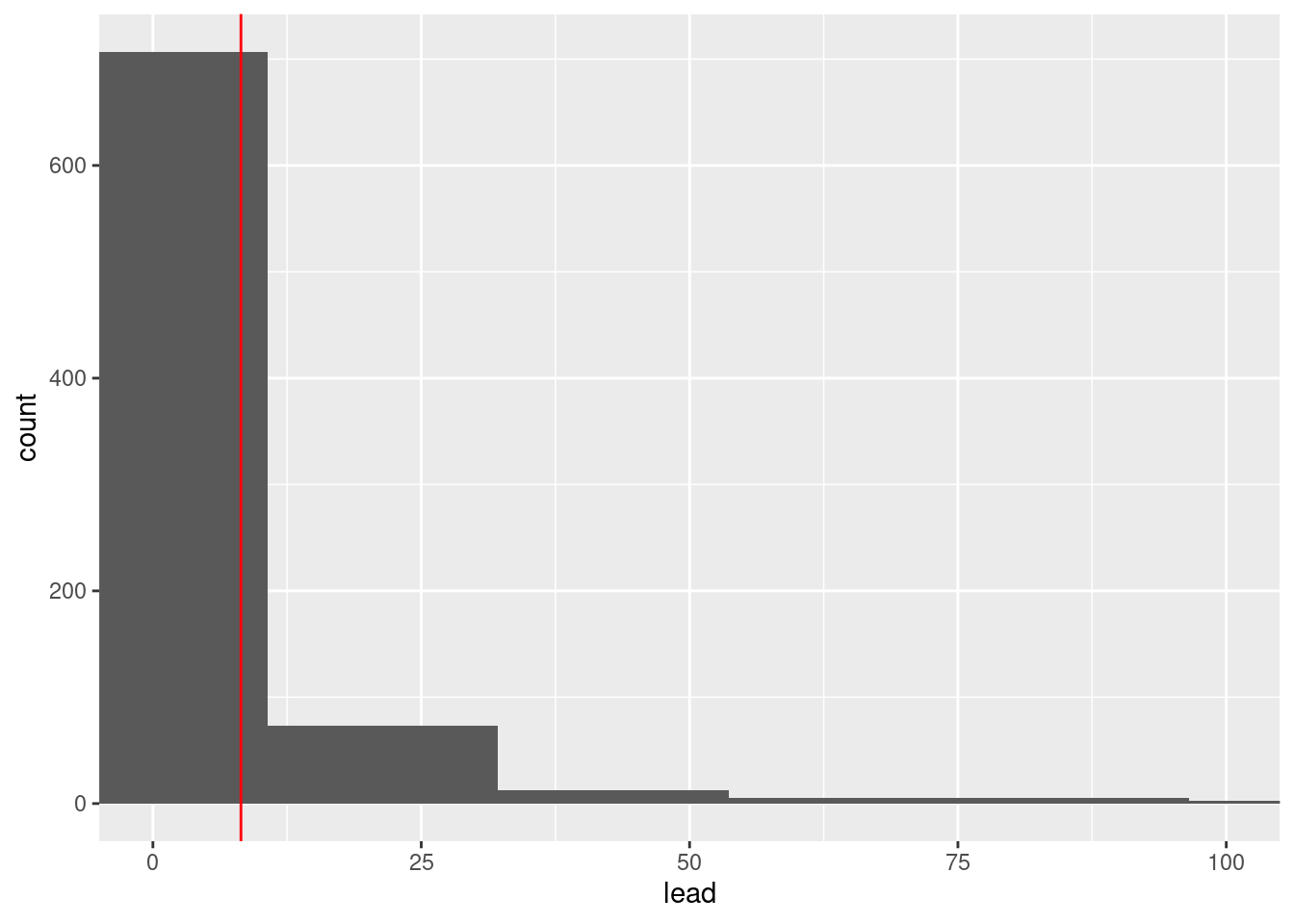

Exercise 6: Add one more layer which overlays the median, in a different color.

ggplot(flint, aes(x = lead)) + 
  geom_histogram(bins = 50) + 
  coord_cartesian(xlim = c(0, 100)) +
  geom_vline(xintercept = summary_table$mean_lead, color = "red") +
  geom_vline(xintercept = summary_table$median_lead, color = "blue")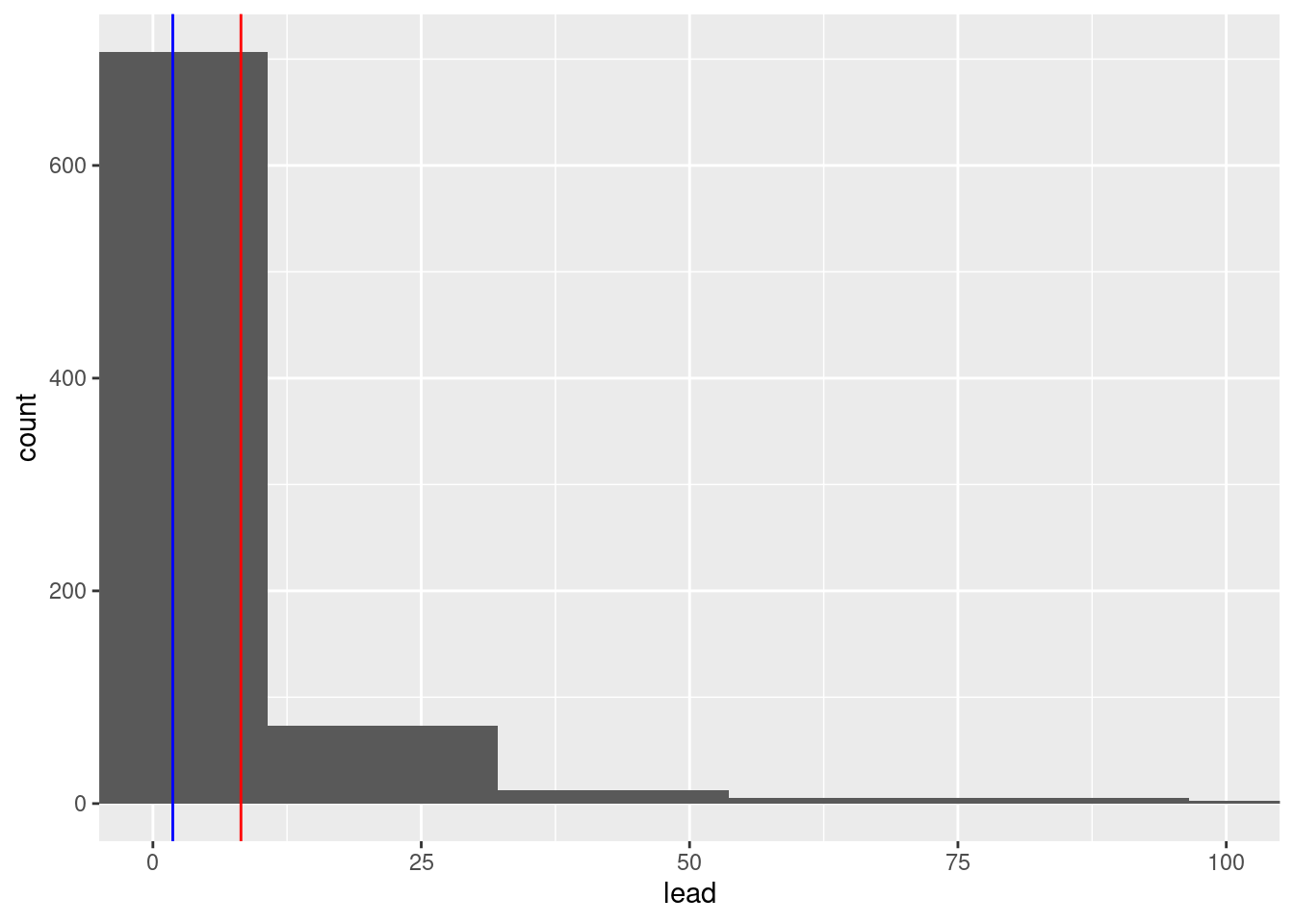

# add code here

Box plots

Next, let’s narrow our focus to the zip codes 48503, 48504, 48505, 48506, and 48507 and observations with lead values less than 1,000 ppb.

flint_focus <- flint |>
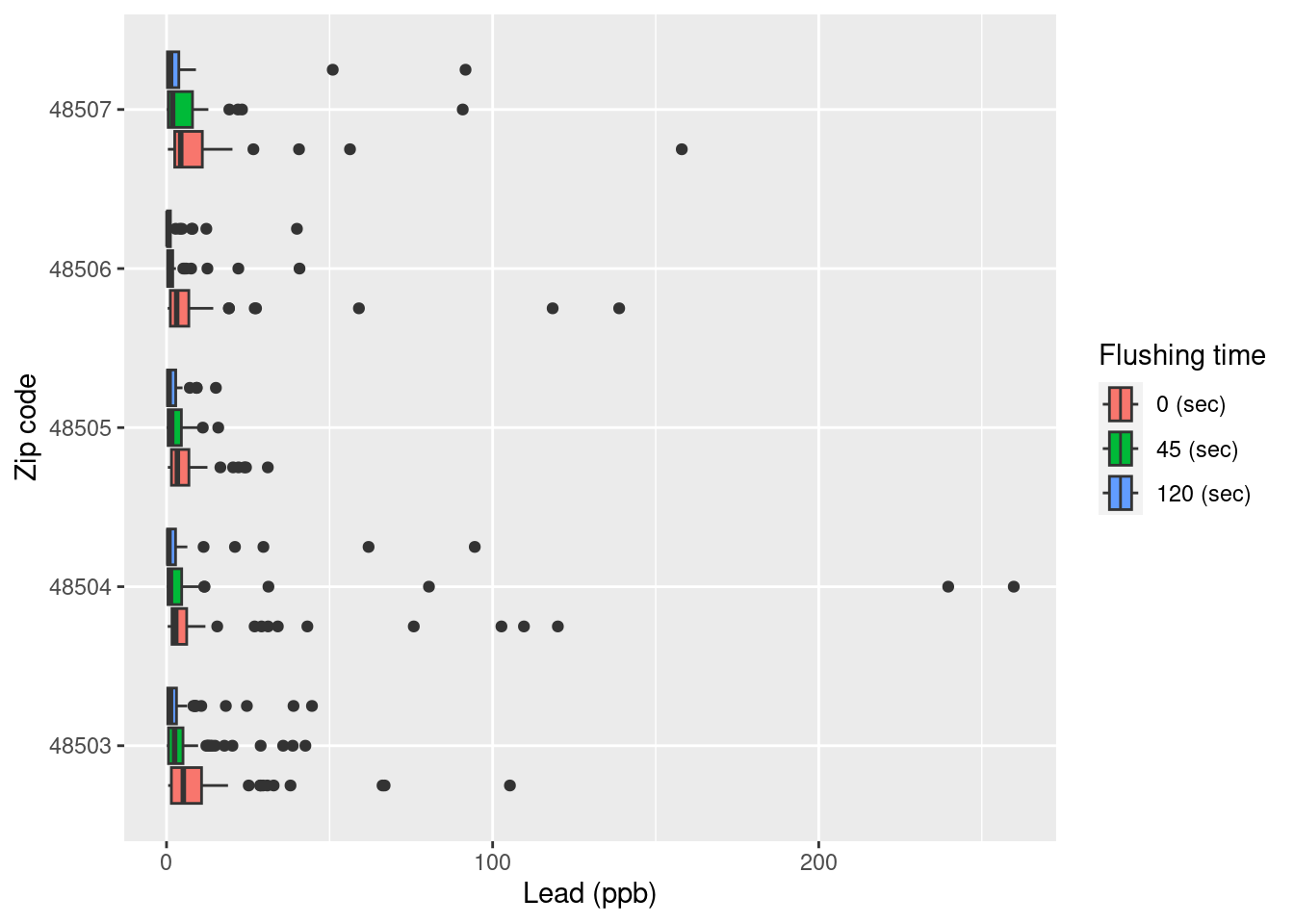
  filter(zip %in% 48503:48507 & lead < 1000)

Exercise 7: Below are side-by-side box plots for the three flushing times in each of the five zip codes we considered. Add x and y labels; add a title by inserting title = "title_name" inside the labs() function.

ggplot(data = flint_focus, aes(y = factor(zip), x = lead)) +
  geom_boxplot(aes(fill = factor(draw))) +
  labs(x = "Lead (ppb)", y = "Zip code", fill = "Flushing time") +
  scale_fill_discrete(
    breaks = c("first", "second", "third"),
    labels = c("0 (sec)", "45 (sec)", "120 (sec)")
  )

Exercise 8: Add labels for x, y, a title, and subtitle to the code below to update the corresponding plot.

ggplot(data = flint_focus, aes(y = factor(zip), x = lead)) +
  geom_boxplot(aes(fill = factor(draw))) + 
  labs(
    x = "Lead (ppb)", y = "Zip code", fill = "Flushing time",
    title = "Lead amount by flushing time",
    subtitle = "In five zip codes"
    ) +
  scale_fill_discrete(
    breaks = c("first", "second", "third"),
    labels = c("0 (sec)", "45 (sec)", "120 (sec)")
  ) +
  coord_cartesian(xlim = c(0, 50)) +
  theme_bw()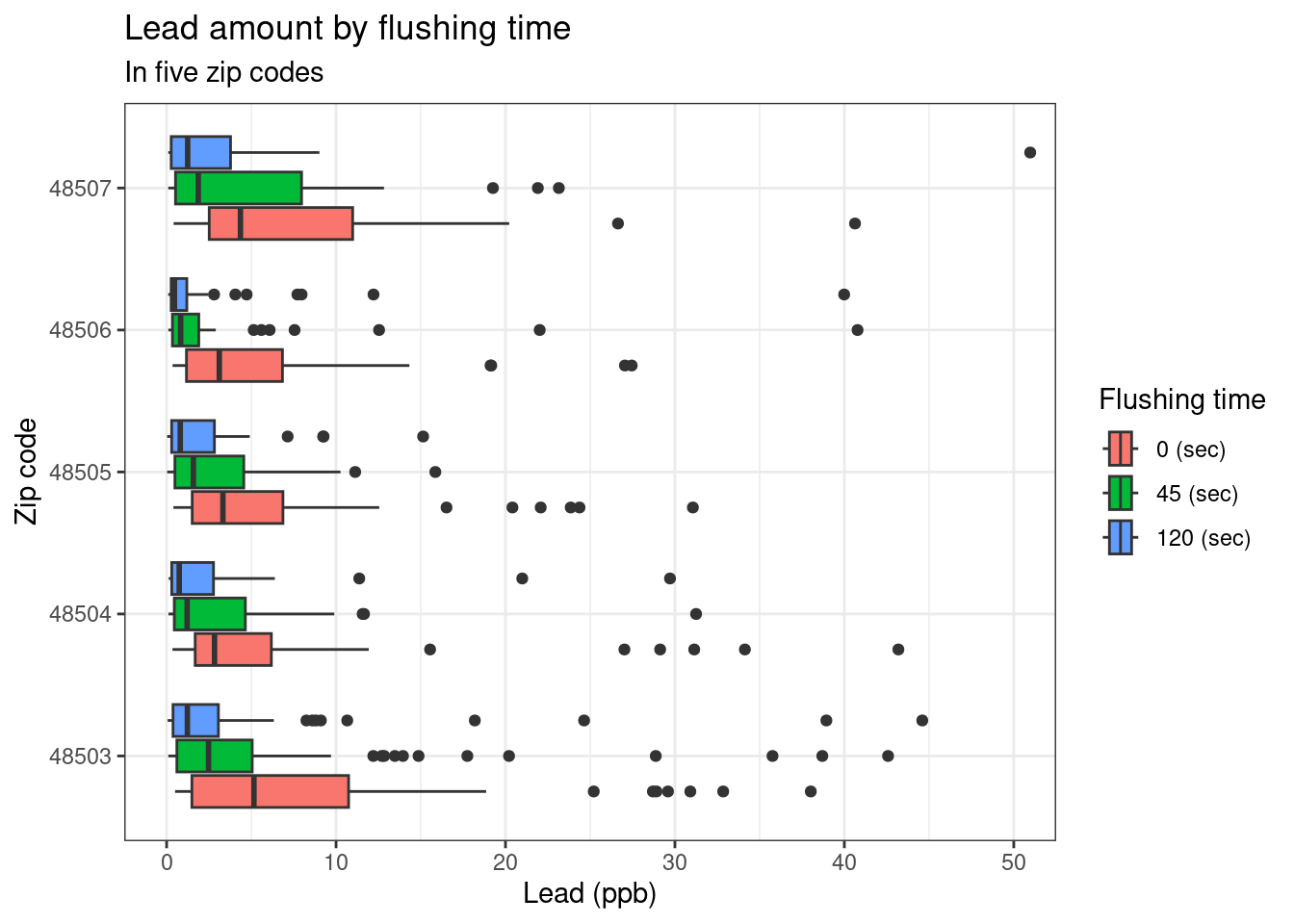

Exercise 9: What is the difference between the two plots? What are the advantages and disadvantages to each plot?

The first plot shows extreme outliers, while the second plot makes it easier to see the bulk of the distribution.

References

  1. Langkjaer-Bain, R. (2017). The murky tale of Flint’s deceptive water data. Significance, 14: 16-21. doi: https://doi.org/10.1111/j.1740-9713.2017.01016.x.

  2. Kelsey J. Pieper, et. al. Evaluating Water Lead Levels During the Flint Water Crisis. Edwards Environmental Science & Technology 2018 52 (15), 8124-8132 doi: https://doi.org/10.1021/acs.est.8b00791.