Exam 1 Review

In 2020, employees of Blizzard Entertainment circulated a spreadsheet to anonymously share salaries and recent pay increases amidst rising tension in the video game industry over wage disparities and executive compensation. (Source: Blizzard Workers Share Salaries in Revolt Over Pay)

The name of the data frame used for this analysis is blizzard_salary and the relevant variables are:

• percent_incr: Raise given in July 2020, as percent increase with values ranging from 1 (1% increase) to 21.5 (21.5% increase)

• salary_type: Type of salary, with levels Hourly and Salaried

• annual_salary: Annual salary, in USD, with values ranging from $50,939 to $216,856.

• performance_rating: Most recent review performance rating, with levels Poor, Successful, High, and Top. The Poor level is the lowest rating and the Top level is the highest rating.

The top six rows of blizzard_salary are shown below:

# A tibble: 409 × 4
   percent_incr salary_type annual_salary performance_rating
          <dbl> <chr>               <dbl> <chr>             
 1          1   Salaried               1  High              
 2          1   Salaried               1  Successful        
 3          1   Salaried               1  High              
 4          1   Hourly             33987. Successful        
 5         NA   Hourly             34798. High              
 6         NA   Hourly             35360  <NA>              
 7         NA   Hourly             37440  <NA>              
 8          0   Hourly             37814. <NA>              
 9          4   Hourly             41101. Top               
10          1.2 Hourly             42328  <NA>              
# ℹ 399 more rows

Question 1

How rows observations are there in the blizzard_salary dataset and what does each row represent?

Question 2

Figure 1 (a) and Figure 1 (b) show the distributions of annual salaries of hourly and salaried workers. The two figures show the same data, with the facets organized across rows and across columns. Which of the two figures is better for comparing the median annual salaries of hourly and salaried workers. Explain your reasoning.

(a) Option 1

(b) Option 2

Figure 1: Distribution of annual salaries of Blizzard employees

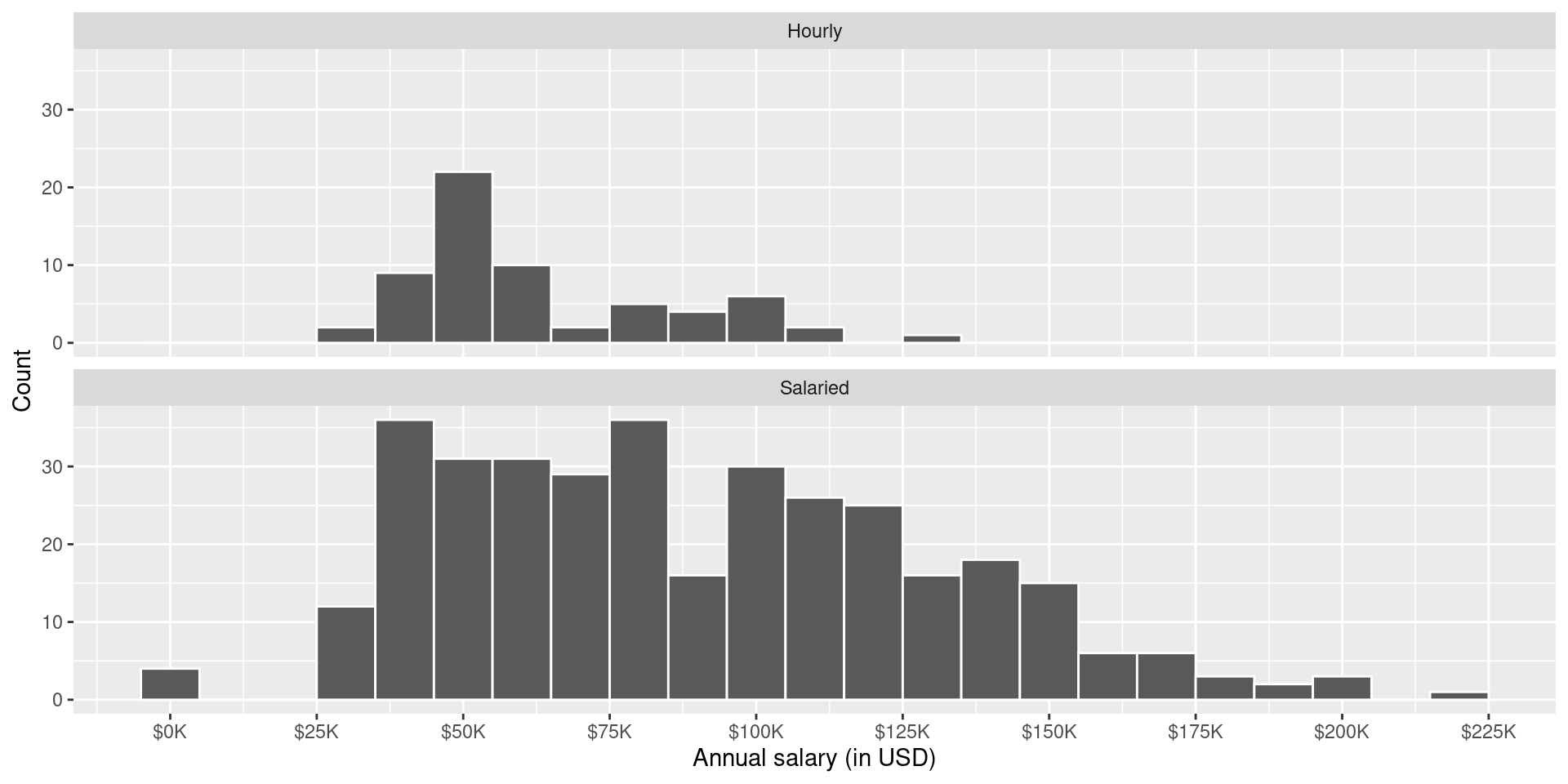
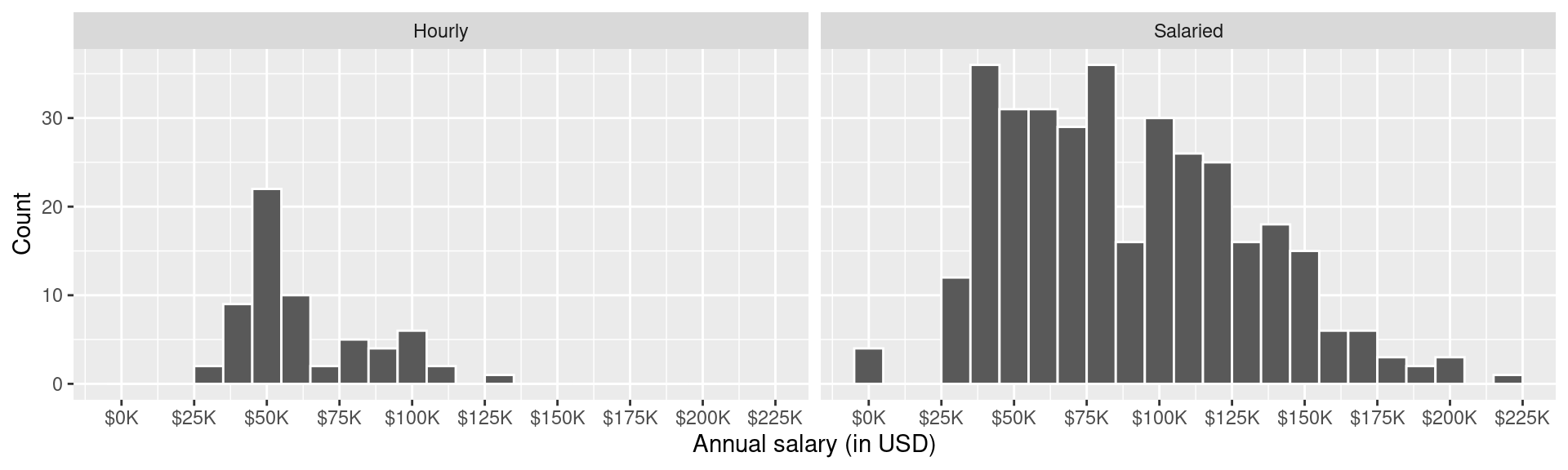
Question 3

Suppose your teammate wrote the following code as part of their analysis of the data.

They then printed out the results shown below. Unfortunately one of the number got erased from the printout, it’s indicated with _____ below.

# A tibble: 2 × 3
  salary_type mean_annual_salary median_annual_salary
  <chr>                    <dbl>                <dbl>
1 Hourly                  63003.               54246.
2 Salaried                90183.               _____

Which of the following is the best estimate for that erased value?

1. 30,000
2. 50,000
3. 80,000
4. 100,000

Question 4

Which distribution has a higher standard deviation?

1. Hourly workers
2. Salaried workers
3. Roughly the same

Question 5

Which of the following alternate plots would also be useful for visualizing the distributions of annual salaries of hourly and salaried workers?

I.  Box plot
II. Density plot
III. Pie chart

1. I
2. I and II
3. I, II, and III
4. II and III

Question 6

Next, you fit a model for predicting raises (percent_incr) from salaries (annual_salary). We’ll call this model raise_1_fit. A tidy output of the model is shown below.

# A tibble: 2 × 5
  term           estimate  std.error statistic   p.value
  <chr>             <dbl>      <dbl>     <dbl>     <dbl>
1 (Intercept)   1.87      0.432           4.33 0.0000194
2 annual_salary 0.0000155 0.00000452      3.43 0.000669 

Which of the following is the best interpretation of the slope coefficient?

1. For every additional $1,000 of annual salary, the model predicts the raise to be higher, on average, by 1.55%.
2. For every additional $1,000 of annual salary, the raise goes up by 0.0155%.
3. For every additional $1,000 of annual salary, the model predicts the raise to be higher, on average, by 0.0155%.
4. For every additional $1,000 of annual salary, the model predicts the raise to be higher, on average, by 1.87%.

Question 7

You then fit a model for predicting raises (percent_incr) from salaries (annual_salary) and performance ratings (performance_rating). We’ll call this model raise_2_fit. Which of the following is definitely true based on the information you have so far?

1. Intercept of raise_2_fit is higher than intercept of raise_1_fit.
2. RMSE of raise_2_fit is higher than RMSE of raise_1_fit.
3. Adjusted \(R^2\) of raise_2_fit is higher than adjusted \(R^2\) of raise_1_fit.
4. \(R^2\) of raise_2_fit is higher \(R^2\) of raise_1_fit.

Question 8

The tidy model output for the raise_2_fit model you fit is shown below.

# A tibble: 5 × 5
  term                            estimate  std.error statistic  p.value
  <chr>                              <dbl>      <dbl>     <dbl>    <dbl>
1 (Intercept)                   3.55       0.508           6.99 1.99e-11
2 annual_salary                 0.00000989 0.00000436      2.27 2.42e- 2
3 performance_ratingPoor       -4.06       1.42           -2.86 4.58e- 3
4 performance_ratingSuccessful -2.40       0.397          -6.05 4.68e- 9
5 performance_ratingTop         2.99       0.715           4.18 3.92e- 5

When your teammate sees this model output, they remark “The coefficient for performance_ratingSuccessful is negative, that’s weird. I guess it means that people who get successful performance ratings get lower raises.” How would you respond to your teammate?

Question 9

Ultimately, your teammate decides they don’t like the negative slope coefficients in the model output you created (not that there’s anything wrong with negative slope coefficients!), does something else, and comes up with the following model output.

# A tibble: 5 × 5
  term                            estimate  std.error statistic    p.value
  <chr>                              <dbl>      <dbl>     <dbl>      <dbl>
1 (Intercept)                  -0.511      1.47          -0.347 0.729     
2 annual_salary                 0.00000989 0.00000436     2.27  0.0242    
3 performance_ratingSuccessful  1.66       1.42           1.17  0.242     
4 performance_ratingHigh        4.06       1.42           2.86  0.00458   
5 performance_ratingTop         7.05       1.53           4.60  0.00000644

Unfortunately they didn’t write their code in a Quarto document, instead just wrote some code in the Console and then lost track of their work. They remember using the fct_relevel() function and doing something like the following:

What should they put in the blanks to get the same model output as above?

1. “Poor”, “Successful”, “High”, “Top”
2. “Successful”, “High”, “Top”
3. “Top”, “High”, “Successful”, “Poor”
4. Poor, Successful, High, Top

Question 10

Finally, your teammate creates the following two plots and ask you for help deciding which one to use in the final report for visualizing the relationship between performance rating and salary type. In 1-3 sentences, can you help them make a decision, justify your choice, and write the narrative that should go with the plot?

(a) Option 1

(b) Option 2

Figure 2: Distribution of salary type by performance rating

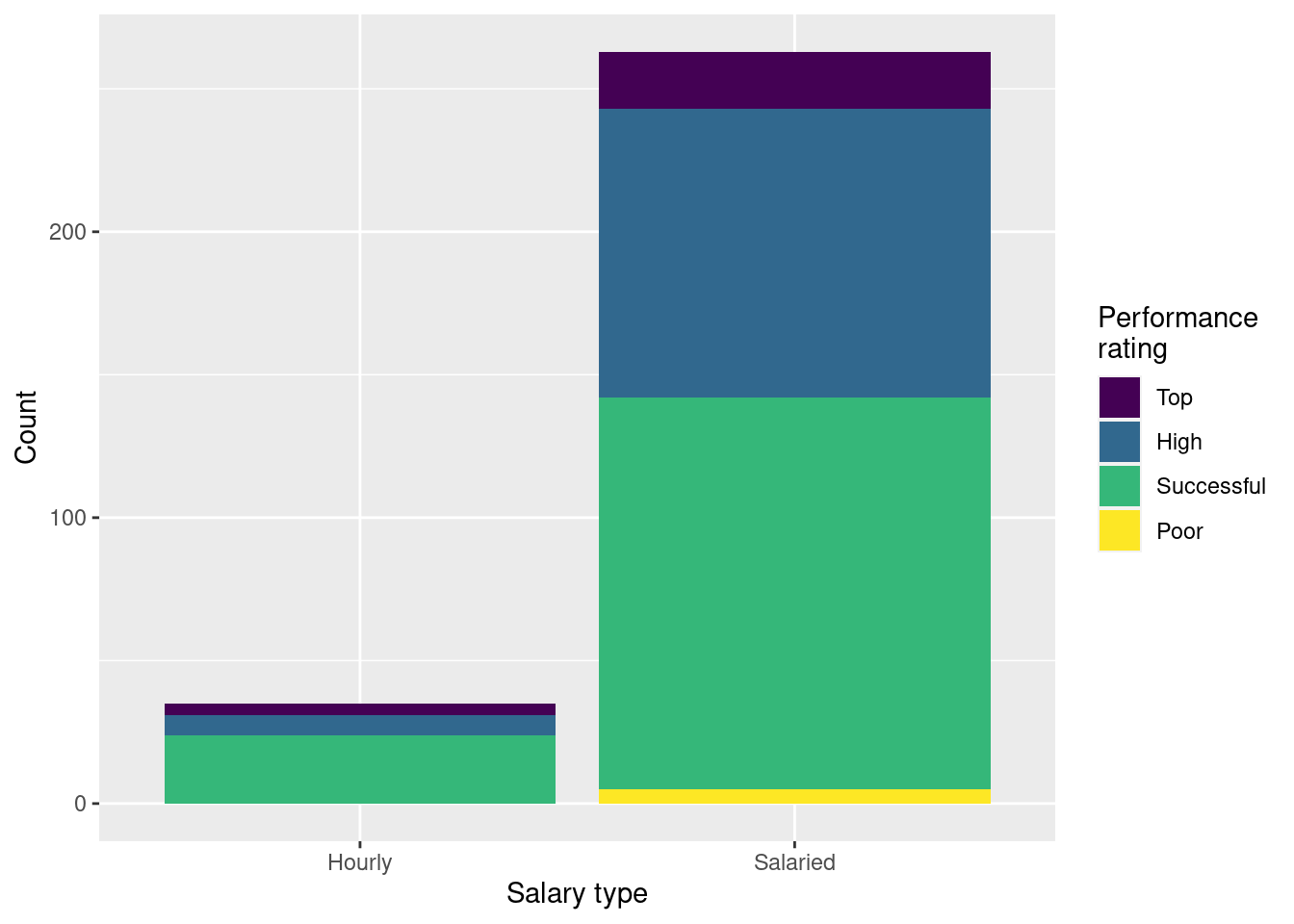
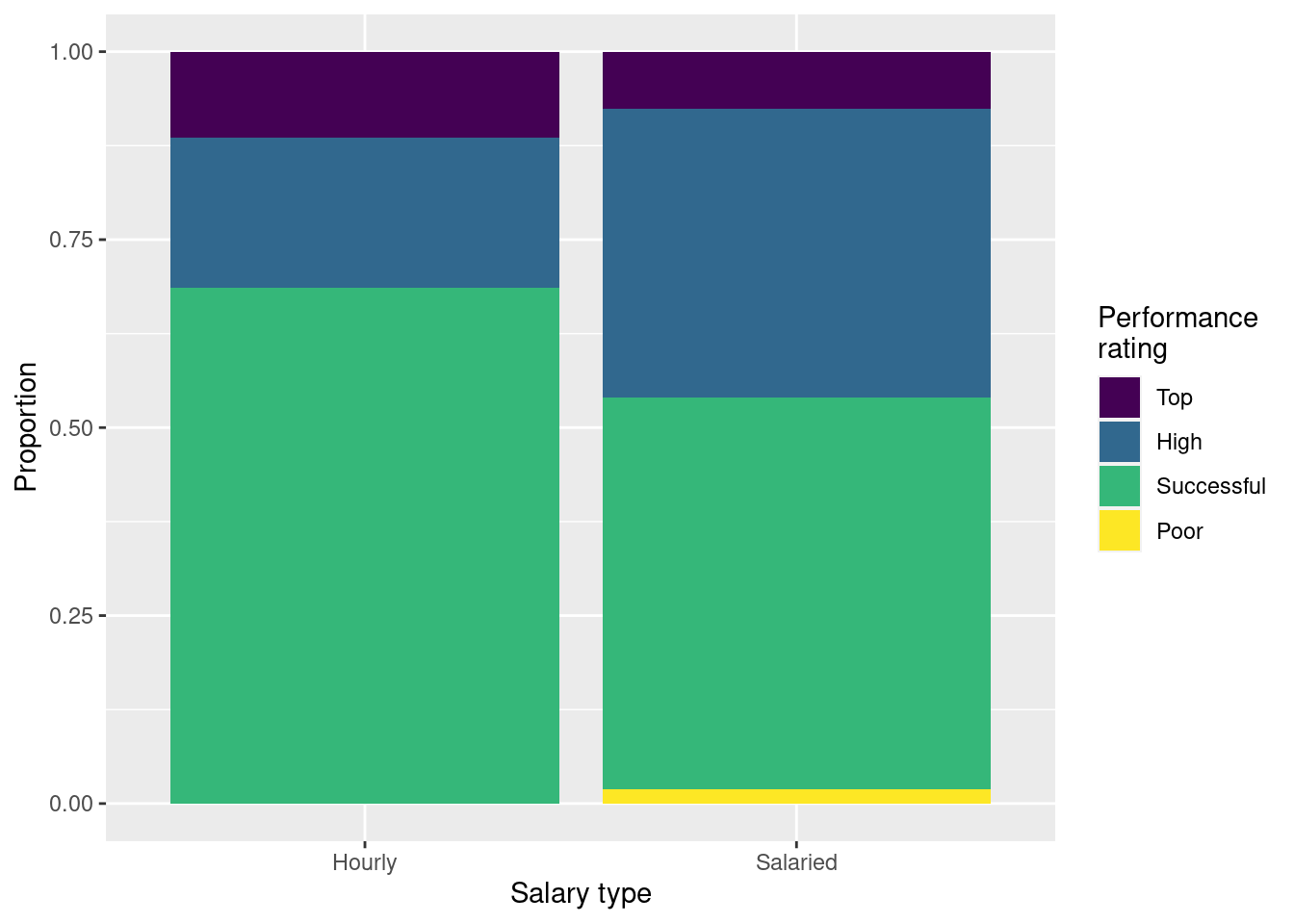
Question 11

A friend with a keen eye points out that the number of observations in Figure 2 (a) seems lower than the total number of observations in blizzard_salary. What might be going on here? Explain your reasoning.

Question 12

Show the proportions of performance ratings for hourly and salaried workers in a table and ask students to place those numbers on the segments of Figure 2 (b).

# A tibble: 4 × 3
  performance_rating Hourly Salaried
  <fct>               <dbl>    <dbl>
1 Successful          0.686   0.521 
2 High                0.2     0.384 
3 Top                 0.114   0.0760
4 Poor                0       0.0190

Question 13

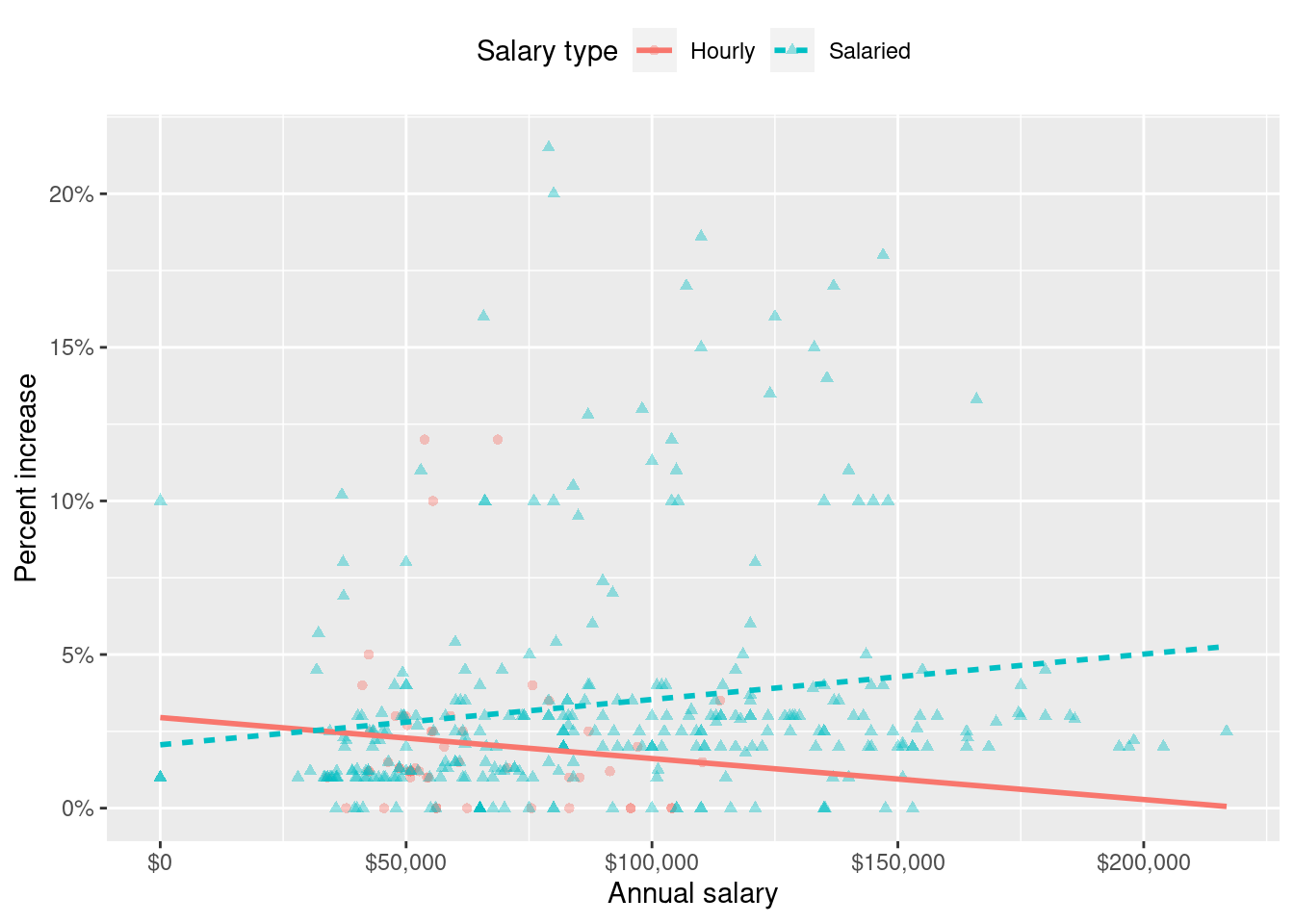
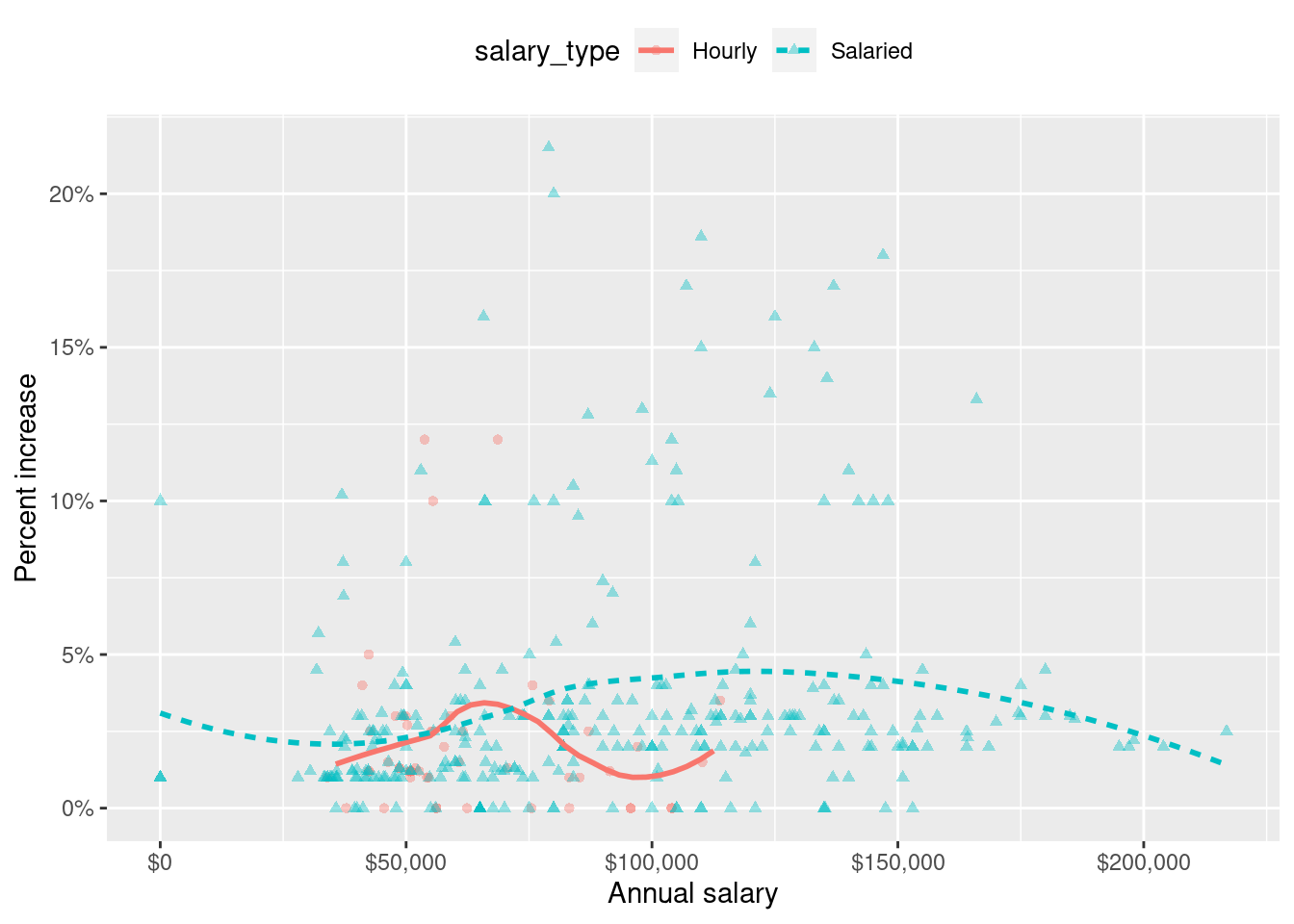
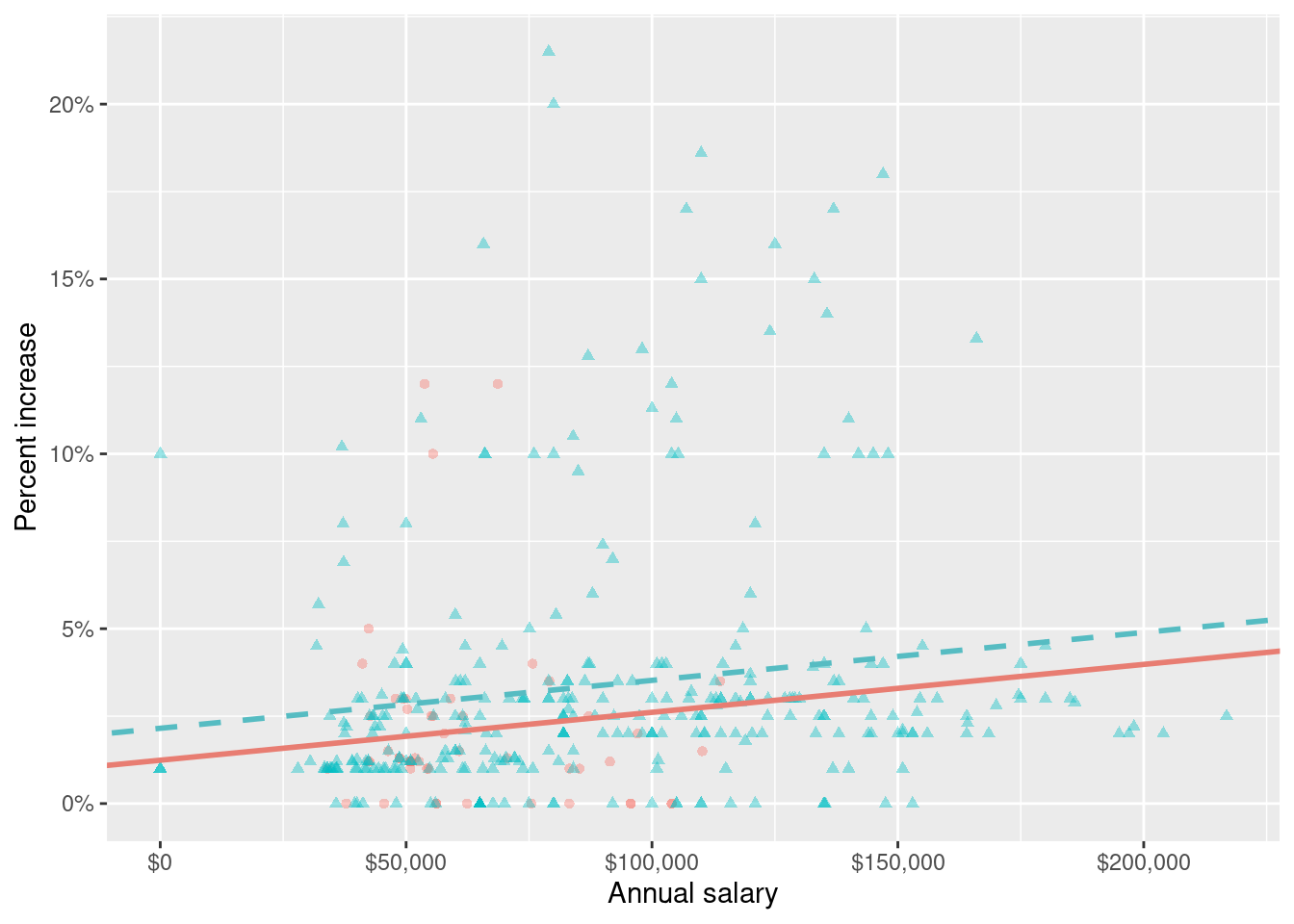
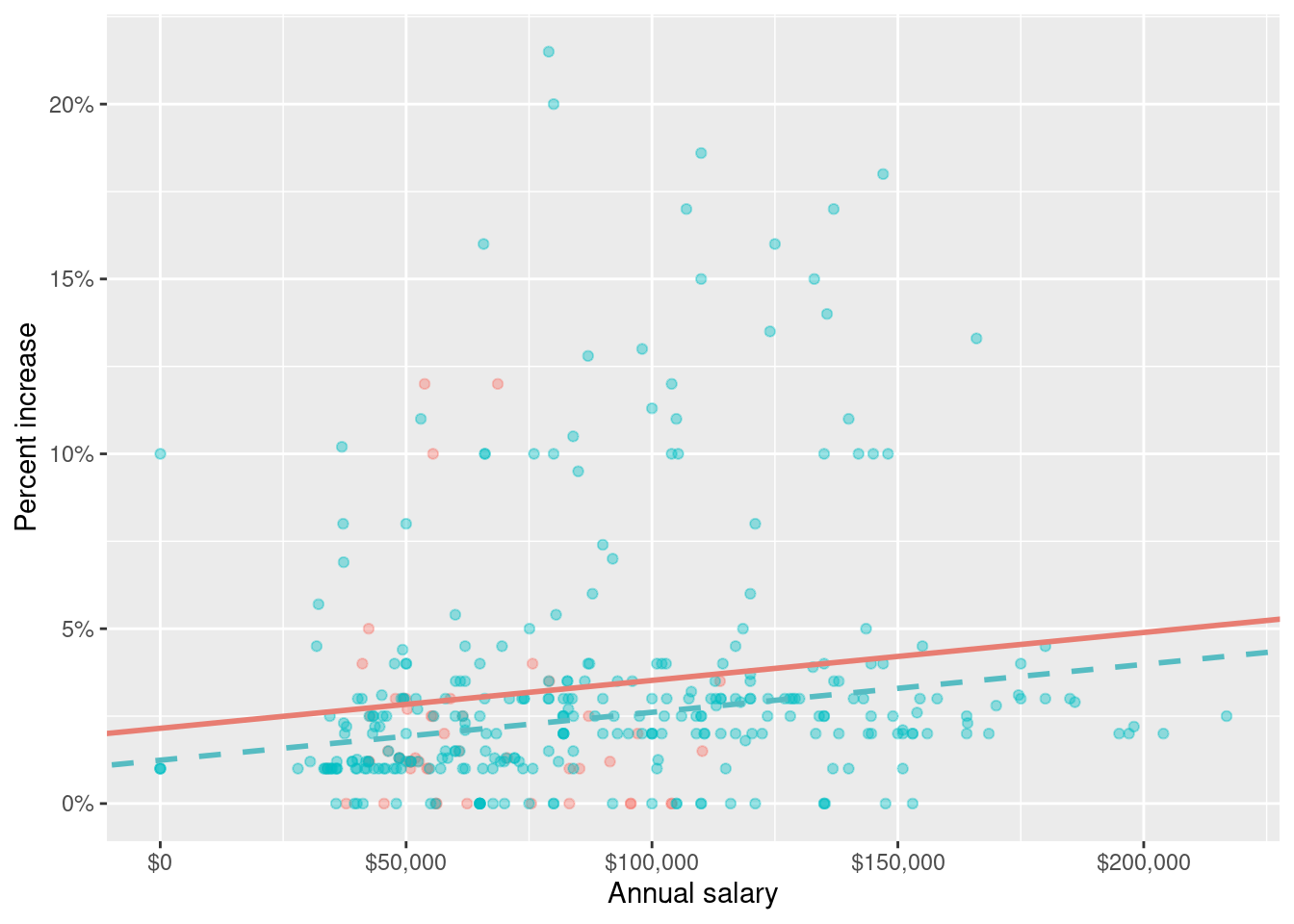
Suppose we fit a model to predict percent_incr from annual_salary and salary_type. A tidy output of the model is shown below.

# A tibble: 3 × 5
  term                 estimate  std.error statistic p.value
  <chr>                   <dbl>      <dbl>     <dbl>   <dbl>
1 (Intercept)         1.24      0.570           2.18 0.0300 
2 annual_salary       0.0000137 0.00000464      2.96 0.00329
3 salary_typeSalaried 0.913     0.544           1.68 0.0938 

Which of the following visualizations represent this model? Explain your reasoning.

(a) Option 1

(b) Option 2

(c) Option 3

(d) Option 4

Figure 3: Visualizations of the relationship between percent increase, annual salary, and salary type

Question 14

A professor gives a test to 100 students and determines the median score. After grading the test, they realize that the 10 students with the highest scores did exceptionally well. They decide to award these 10 students a bonus of 5 more points. The median of the new score distribution will be ____ the original median.

1. , depending on skewness, higher or lower than

2. equal to

3. lower than

4. higher than

Movies

The data for this part comes from the Internet Movie Database (IMDB). Specifically, the data are a random sample of movies that were released between 1980 and 2020.

The name of the data frame used for this analysis is movies:

movies <- read_csv("movies.csv")

It has 600 observations and 16 variables. However, for the in-class part of this exam we’ll only work with a subset of these variables:

• name: name of the movie
• genre: main genre of the movie
• runtime: duration of the movie (in minutes)
• release_country: release country
• score: IMDB user rating

Below is a peek at these variables:

movies |>
  select(name, genre, runtime, release_country, score)

# A tibble: 600 × 5
   name                                genre     runtime release_country score
   <chr>                               <chr>       <dbl> <chr>           <dbl>
 1 Malice                              Crime         107 United States     6.4
 2 Beach Rats                          Drama          98 Sweden            6.4
 3 The Souvenir                        Drama         120 United Kingdom    6.4
 4 All or Nothing                      Drama         128 United Kingdom    7.5
 5 The Final Destination               Action         82 United States     5.2
 6 Harry Potter and the Goblet of Fire Adventure     157 United States     7.7
 7 The Duke of Burgundy                Drama         104 United States     6.5
 8 Multiplicity                        Comedy        117 United States     6.1
 9 The Bad Batch                       Action        118 United States     5.3
10 Brainscan                           Comedy         96 United States     6.1
# ℹ 590 more rows

Question 15

Suppose we want to modify the release_country variable such that the levels are “United States” and “not United States”. Fill in the blanks in the code chunk below to accomplish this.

movies____________movies |>
      ____________(
        release_country = if_else(
        release_country____________"United States", 
        "____________",
        "____________"
        )
)

Question 16

A researcher wants to build a multiple linear regression model to predict the score of a movie in from runtime for the movies in different types of genre.

The total sum of squares for the model \(SS_{Total}\) is found to be 0. You know that:

1. every runtime in every genre had the same amount
2. every movie had the same score
3. the model perfectly predicts score in every movie
4. the mean score must be 0

Question 17

Choose the best answer.

A survey based on a random sample of 2,045 American teenagers found that a 95% confidence interval for the mean number of texts sent per month was (1450, 1550). A valid interpretation of this interval is

1. 95% of all teens who text send between 1450 and 1550 text messages per month.
2. If a new survey with the same sample size were to be taken, there is a 95% chance that the mean number of texts in the sample would be between 1450 and 1550.
3. We are 95% confident that the mean number of texts per month of all American teens is between 1450 and 1550.
4. We are 95% confident that, were we to repeat this survey, the mean number of texts per month of those taking part in the survey would be between 1450 and 1550.

Premature babies

Suppose you are given a dataset with the following variables:

Codebook:

m_age

Mother’s age.

weeks

Weeks at which the mother gave birth.

premature

Indicates whether the baby was premature or not.

weight

Birth weight of the baby (lbs).

Smoke

Whether or not the mother was a smoker.

Question 18

1. Write the theoretical model that regresses weight on m_age, weeks, and premature. Be sure to define each term (i.e., \(y= -----\)).

Then, using the output below, write the fitted model.

# A tibble: 4 × 5
  term            estimate std.error statistic     p.value
  <chr>              <dbl>     <dbl>     <dbl>       <dbl>
1 (Intercept)      -4.35      2.10       -2.07 0.0404     
2 m_age             0.0270    0.0142      1.90 0.0594     
3 weeks             0.281     0.0509      5.52 0.000000153
4 prematurepremie  -1.01      0.398      -2.54 0.0121     

2. Interpret the intercept, in 1 sentence.

3. Interpret the slope for premie, in 1 sentence.

Bonus

Pick a concept we introduced in class so far that you’ve been struggling with and explain it in your own words.